9.30

특이값 분해 -> 특잇값 분해를 이용해 성능을 향상시킬 수 있는 알고리즘 제작

5-1 행렬과 좌표변환

좌표변환이란 이차원 평면위에 x,y가 f를 통해서 어디로 이동하는것.

f 는 1차식일때만 됨( 지수 , 로그 등등 ㄴㄴ해)

위에서 중간의 행렬은 계수로 구성되게 된다.

위로 3배 늘린당

이 예는 가로,세로로 찌그러지는건 아니다.

(1, 1)은 같은 방향으로 3배 늘어나게 된다. =>(3,3)이 되니깐.

Q. 행렬이 하나 주어지는데 그 행렬가지고 좌표변환을 합니다. 

이 행렬이 어떻게 주어지던 간에 어떤 방향으로 확대한것으로 이해할수있는가

그림으로 그리자면 예에 대해서 두 방향으로 더했더니 각각의 방향으로 확대,축소로 이해할수있는가

5-2 특이값 분해

좌표변환을 생각하자 ( 행렬을 가지고) 

우리가 원하는건 만약 1,0  0,1 에서는 확대 축소 의미로 안될수 있음

만약 방향을 바꿔서 각 각의 방향으로 확대,축소로 가면 그 주어진 행렬을 어떻게 쪼개는가

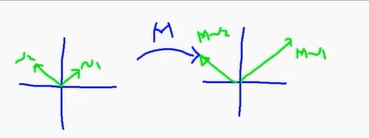
v1 방향으로 정확히 가진않지만 수직이라서 ㄱㅊ

회전하는것도 행렬로 할수가 있당.

고로 결론 => 두 방향이 수직인데 변환하고 나서도 수직인거를 찾을수가 있는가(회전 가능)

보냈을때 적당한 상수배가 된다.

아니라면 차선책으로  적당히 회전한다.

V1을 M으로 변환 된것은 해당 방향의 u1이라는 기본단위가 시그마 만큼 커진것이다.

 

5-3

왼쪽의 그림을 오른쪽의 3개가지고 표현할 수있다.

식이 복잡해서 손으론 할수가 없다.

v를 m으로 보냈더니 u의 시그마 배가 되었다.

v1,v2,v3는 15개의 데이터 3개만 있으면 된다.

25개는 ui의 정보 , ui 3개, 시그마도 3개만 있으면 됨 

이걸 합치면 M이 된다.

고로 정보를 기억하는 횟수가 3배 줄어든다.

 

그림은 사람이 이해하는 정도까지라면 흐릿하게 만드는게 편함

(데이터가 줄어들기 떄문)

jpg는 손실압축이당.

커다란 호랑이 그림을 적당한 행렬로 표현할 수 있다

특이값= v를 보냈을때 얘가 어떻게 가느냐 u방향으로 시그마 이떄의 시그마가 특이값.

계산하였을떄 시그마가 너무 작다면 작은값이므로 무시해도 된다.

고로 무시하고 계산하였을떄 기존의 M과 동일하진 않아도 그래도 M과비슷한 데이터가 될것이다.

이걸 전문용어를 rank라고 한다

rank200 이란건 시그마 1 부터 시그마200까지만 고려

 

잡음제거

잡음이 없으면 0과1로만 구현되있지만 잡음이 있으면 그건 0.7 0.3 이런식으로 있을거다.

이떄 특이값 분해를 사용할 수있다.

위에 3개만 하고, 아래는 무시가능한 정도로 크기가 작다.

직선 데이터를 찾고싶다. 

이 데이터를 행렬로 표현한다. x와 y를 세로로 늘어놓음

그리고 이 행렬의 특이값을 계산한다. 두번쨰 값이 굉장히 작고, 우리는 직선을 찾고싶은거라서

첫번쨰 까지만 생각한다. rank 1만 생각한다. 

rank1이란? => 직선

netflix 알고리즘

1. 영화를 보면 그 영화 평가함

2. 비슷한 평가를 한 사람들끼리 무리를 지음

=> 그 무리짓는 방법이 특이값 분해

3.그 무리에서 높은 평가를 받은 영화를 추천한다.